La inversión en letras del Tesoro: una gran oportunidad, pero con conocimiento. La paradoja explicada de las letras a 9 y 12 meses

Por Carlos Perelló, profesor del PE en Derecho de los Mercados Financieros y socio de Perelló&Biosca&Cabrera SLP.

Hace unos días el Gobierno de España a través del Tesoro emitió letras a 9 meses (L9) y Letras a 12 meses (L12) donde las primeras, con vencimiento anterior, salieron a un tipo medio superior a las de 12 meses, 2,938% las primeras contra 2,813% las segundas.

Se comentó en varios medios financieros lo que, supuestamente, significaba que el Tesoro español pagara más por un  vencimiento inferior, L9, que uno superior, L12, y se dijo que era porque se esperaba que los tipos cayeran a partir de esos 9 meses. Ya decimos que esta explicación no es correcta.

La explicación es mucho más sencilla pero antes de darla vamos a dar unas pequeñas nociones de los mercados financieros.

 

La percepción del riesgo en los mercados

Hay dos principios básicos de los mercados que SIEMPRE se cumplen ya que, de no cumplirse el mercado, se ajustaría tan rápidamente que volverían a cumplirse y son:

1º A mayor riesgo mayor rentabilidad. De lo contrario los inversores venderían lo más arriesgado y comprarían lo menos y encima obtendrían un mayor rendimiento. No es posible.

2º “There is no free lunch” o en su versión española “nadie da duros a cuatro pesetas” porque si así fuera todos haríamos este cambio hasta que el lado contrario, el que da los duros, no tuviera ya más que dar. Tampoco es posible.

Decir que la percepción del riesgo de los activos NO es “tu” percepción sino la del mercado en su conjunto. Uno puede tener mejor percepción que el mercado y ganar un buen dinero pero no suele ser muy habitual que uno tenga razón y el resto del mundo, el mercado en su conjunto, se equivoque (no es imposible pero mejor pensar que no es así). Y cuando se hacen análisis comparativos de activos se deben hacer en el mismo momento y usando los mismos datos comunes.

Es cierto que a los Mercados de Capitales les “encanta” atacar dogmas y verdades absolutas para demostrar quién manda en los mercados pero es, en general, bastante ortodoxo porque el dinero, como sabemos, es asustadizo.

Hablando ahora de las Letras o emisiones a corto plazo (hasta 12 meses) de países desarrollados tipo UE, EEUU, Japón, Suiza, UK, Suecia, Dinamarca, Noruega etc decir que tienen en común lo siguiente:

• Se considera que su riesgo de impago es nulo o cercano a él.
• En las Letras de un país, predomina el inversor doméstico, sea éste sus bancos, los fondos monetarios o los inversores privados. Los inversores internacionales pedirán siempre una prima mayor por invertir en otro país aunque el riesgo sea el mismo.
• No existe realmente un mayor riesgo o menor liquidez porque sean Letras a 3 meses o 12 meses.
• Su rentabilidad se deriva de los tipos de política monetaria que fije el banco central de su propia moneda, por tanto para las Letras Españolas, Italianas, Alemanas, Francesas, Portuguesas etc su rentabilidad depende de la política monetaria del BCE.
• Si no hubiera un “sesgo” doméstico importante, o costes de transacción/transferencia diría que las letras a 3 meses de todos los países de la EU deberían estar al mismo tipo. De hecho, a 15 de Febrero 2023 están todas (de los países de la UE arriba mencionados) en torno al 2,60% excepto la española, curiosamente, algo más baja. A 12 meses están en torno al 3/3.10% excepto la italiana algo más alta. En principio esta diferencia es por el sesgo doméstico, por el volumen de emisión y la necesidad de inversores internacionales.

Para nuestro análisis vamos a pensar que todas las letras de los países de la EU deberían dar la misma rentabilidad. Vamos a considerar inicialmente (luego usamos la práctica de mercado) que el año son 360 días y que los meses tienen 30 días para  cálculo de intereses y no vamos a tener en cuenta los diferenciales de demanda/oferta o pequeños factores que puedan hacer variar algo el precio. La idea es de mostrar cómo se forman los precios de las Letras y por qué sucedió lo que sucedió con las emisiones de las L9 y L12 últimas realizadas en España.

 

Los tipos de interés del BCE

Ahora hablemos del tipo que fija el Banco Central Europeo (BCE). El BCE fija un tipo de interés en cada reunión monetaria y este tipo se mantiene sin cambios (excepto cataclismo) hasta la siguiente reunión (normalmente mensual, a veces dos meses más o menos). En 2023 hay 8 reuniones del BCE para fijar tipos de interés.

El BCE fija 3 tipos de interés pero el que nos interesa para las Letras es el tipo de Facilidad de Depósito que el la rentabilidad que obtienen las entidades financieras por depositar a 1 día su liquidez en el Banco Central y que actualmente es del 2,50% para toda la UE. Por tanto, si un banco espera que los tipos no se muevan en 3 meses se puede obtener 2,50% diariamente o se puede invertir a una Letra a 3 meses que pagará alrededor de este 2,50%. Las letras a 3 meses no pueden estar por debajo de ese 2,50%, en términos generales, porque si se espera que los tipos se mantengan a ese 2,50% los bancos prestarían su liquidez diaria al 2,50% en vez de invertir en una Letra a 3 meses por debajo de ese nivel.

Por tanto, tenemos un tipo diario que marca el BCE y a partir de este nivel y sus expectativas de variaciones en el futuro se da una rentabilidad a las Letras a 3/6/9/12 meses. De hecho, es esta misma técnica la que, implícitamente, da la rentabilidad de los Bonos de Gobierno, sobre todo de Alemania como el activo benchmark sin riesgo de la UE, aunque he de decir que para vencimientos > 5 años entran en funcionamiento otros factores macro como objetivo de Inflación, independencia del Banco Central, productividad y crecimiento poblacional. Y una vez tengamos los tipos alemanes valoramos la curva francesa, española, italiana etc en función de la prima de riesgo que el mercado quiera poner. Prima de riesgo que es muy baja, tendiente a cero hasta 12 meses y a partir de ahí sube con el tiempo por las incertidumbres. Pero todo esto daría para un libro, volvamos a concentrarnos en las Letras hasta 12 meses.

 

Tres ejemplos de cómo influye la política monetaria sobre las letras

Vamos a dar algunos ejemplos de cómo se valoran las letras utilizando medias simples en vez de capitalizaciones que veremos luego.

Ejemplo 1: El mercado espera que los tipos, hoy al 2,50%, no se muevan en 1 año con probabilidad 100% entonces toda la curva estaría plana desde el depósito a 1 día hasta la L12 y todo al tipo 2,50%.

Ejemplo 2: El mercado espera que los tipos, hoy al 2,50%, suban al 3% al final de los primeros 3 meses y luego al 3,50% al final del mes 6 y al 4% al final del mes 9 ¿cómo deberían cotizar estas letras utilizando medias simples?

La L3 cotizaría al 2,50% porque es como están los tipos esos primeros 3 meses.

La L6 cotizaría al 2,75% porque se espera obtener un 2,50% los primeros 3 meses y 3% los segundos 3 meses, la media de rentabilidad en los 6 meses es de 2,75%.

La L9 cotizaría al 3% porque se espera ganar 2,50% los primeros 3 meses, 3% los segundos 3 meses y 3,50% el tercer trimestre, la media es 3%.

La L12 cotizaría al 3,25% porque se espera ganar 2,50% los primeros 3 meses y 3% los segundos 3 meses, 3,50% el tercer trimestre y 4% el cuarto trimestre, la media es 3,25%.

Como vemos tenemos una curva con pendiente positiva entre L3 y L12 porque se espera que los tipos suban.

Pongamos ahora un ejemplo que explicaría que la L9 pagara más que la L12:

Ejemplo 3: El mercado espera que los tipos, hoy al 2,50%, suban al 3% al final de los primeros 3 meses y luego al 3,50% al final del mes 6 y caigan al 2,5% al final del mes 9 ¿cómo deberían cotizar estas letras?

La L3 cotizaría al 2,50% porque es como están los tipos esos primeros 3 meses.

La L6 cotizaría al 2,75% porque se espera obtener un 2,50% los primeros 3 meses y 3% los segundos 3 meses, la media de rentabilidad en los 6 meses es de 2,75%.

La L9 cotizaría al 3% porque se espera ganar 2,50% los primeros 3 meses, 3% los segundos 3 meses y 3,50% el tercer trimestre, la media es 3%.

La L12 cotizaría al 2,875% porque se espera ganar 2,50% los primeros 3 meses, 3% los segundos 3 meses, 3,50% el tercer trimestre y 2,50% el cuarto trimestre, la media es 2,875%.

Como vemos aquí la pendiente es positiva hasta los 9 meses y luego negativa porque el mercado espera (con o sin razón, esto ya se vería) que el BCE baje tipos de 3,50% a 2,50% en el cuarto trimestre.

Si analizamos este último ejemplo con los tipos de la L9 y L12 que se subastaron en España la semana pasada (los días 14 y 7 de febrero respectivamente) que salieron a tipos medios de 2,938% (L9) y 2,813% (L12) pudiera parecer que es exactamente lo que pasó y por eso el medio económico comentó que la razón de una curva de tipos invertido entre la L9 y L12 fue que el mercado esperaba que los tipos bajaran a partir del mes 9. ¿Es esto cierto?

Desgraciadamente, debo decir que en absoluto fue lo que pasó!!

 

Diferencias entre la teoría de mercado y la realidad

Estos ejemplos están realizados de una manera simple, utilizando medias aritméticas simples para los tipos y fechas de reuniones de la BCE para modificar tipos cada 3 meses cuando la realidad es algo más complicada pero no mucho más y la diferencia no es tan grande. ¿Qué diferencias observamos entre estos ejemplos con la realidad?

1. El mercado no utiliza medias aritméticas.

2. Expectativas. Las modificaciones de tipos se producen realmente en fechas de reuniones de la BCE y las expectativas de mercado se conocen porque hay productos que los cotizan como el €STR OIS (que no vamos a explicar aquí) pero también leyendo la prensa/internet es fácil saber cuáles son las expectativas del mercado. Por otro lado, el propio BCE (y la FED) dan sus propias expectativas (que no tienen por qué cumplirse porque ni ellos tienen una bola de cristal) y las expectativas del BCE sobre qué van a hacer ellos mismos a veces no coincide con lo que el mercado piensa sobre qué es lo que van a hacer. Esto es, el mercado descuenta a veces que el BCE no va a poder hacer lo que el propio BCE cree que va a hacer. Curioso pero es así.

3.- Los días que hay en cada Letra no son siempre los mismos ya que algunos trimestres pueden tener 92 días y otros 91 o incluso 89. La Base de Cálculo de intereses es de Actual/360, es decir el exacto número de días entre fecha de emisión (no de subasta) y fecha de vencimiento dividido por 360 (lo cual es mejor para el inversor). Pongamos un ejemplo, la última letra de 9 meses se emitió con estos datos:

• Fecha subasta: 14/02/2023
• Producto: Letras del Tesoro a 9 meses
• Fecha de emisión: 17/02/2023
• Fecha de amortización o vencimiento: 10/11/2023
• Tipo de interés medio: 2,938 %
• Precio medio de compra por título: 978,76 €

Entre la fecha de emisión 17 Feb y la fecha de vencimiento 10 Nov hay 266 días exactamente (por eso se llama Actual), el tipo de interés medio fue 2.938%. Si invertimos 1000€ veamos a qué precio compro la Letra utilizando la fórmula siguiente:

Inversión = Nominal Invertido / (1+tipo medio * A/360) , sustituyendo

Precio de compra L9 = 1000 / (1+0.02938 *266/360) = 978.76€

4.- Pago de intereses: Las Letras pagan intereses a descuento, es decir, a diferencia de los Bonos, los intereses en una Letra son descontados de tu inversión inicial y recibes tu nominal invertido a vencimiento. En los Bonos inviertes el nominal exactamente y recibes el cupón del Bono anualmente (puede ser semestral también en ciertos países) y el nominal a vencimiento, además el cálculo de intereses de los Bonos es 30/360 es decir la base de cálculo es menos favorable al inversor. Digamos que en un año de 365 días, vamos a comparar una letra a 12 meses con un Bono de 1 año y ambos se publicitan con una rentabilidad del 3% y el cupón del Bono es 3%.

¿Qué intereses paga cada activo por una inversión de 1000€?

Bono: 1000 + 1,03 = 1030€ . El inversor recibe 30 euros a vencimiento de intereses.

Letra: Precio saldría 970.481€ (fórmula de arriba) . El inversor recibe 29.519 euros a vencimiento (menos que en el Bono, pero tiene truco). Si mi inversión es la misma, es decir invierto 1000€ exactamente en la letra (como en el Bono) el Precio en la fórmula es 1000€ y mi nominal debería ser 1030.417€. Invierto un nominal de 1030.417€ para desembolsar exactamente 1000€ y por tanto mis intereses son 30.417€ (más que en el Bono). Si bien parece poco, menos de medio euro en 1000€, hablamos de casi 417.000€ más de intereses para una inversión de 1000 Millones de €. El mercado está claro que sabe esto y por tanto el interés de la letra en circunstancias normales sería menos que en el Bono para que no hubiese “free lunch”, la letra saldría a un interés de 2,959%. Si ahora invertimos 1030 euros de nominal en la Letra a este tipo del 2,959% (inferior al 3% del bono) sale que el Precio es 1000€, es decir, invertimos 1000€ en la Letra para recibir 1030€ a vencimiento exactamente igual que el Bono, esto es, la manera de pagar intereses y la base de cálculo hace que el 3% de un Bono a 1 año sea igual que el 2,959% de una Letra a 12 meses.

Por tanto si un inversor quiere realmente invertir 1000€ en Letras debe comunicar un nominal superior en función del plazo de la Letra y del interés que cree va a salir. Un buen proxy es multiplicar la cantidad en Euros que se quiere realmente invertir por 1 + el interés esperado en la Letra multiplicado por el plazo en años (0,25 si es L3, 0,5 si es L6, 0,75 si es L9 y 1 si esL12). Es decir si quiero invertir realmente 1000 euros en una L9 y espero que salga un interés del 2,90% debiera comunicar un nominal de inversión de 1000*(1+2,90%*0,75) = 1021,75€. De esta manera invertiré 1000€ exactamente y recibiré 1021,75€ a vencimiento (recordad que es un proxy y hay que saber más o menos por dónde va a estar el tipo de interés implícito en la Letra que se va a emitir, si se hace bien la diferencia con la realidad será mínima). De hecho si cogemos los datos de la L9 de arriba mencionada el montante exacto que habría que haber dicho de nominal sería 1021,71€ en vez de 1021,75€ , como veis la diferencia es mínima y el cálculo más rápido.

5.- Fiscalidad. Las Letras, como la mayoría de activos financieros, reciben intereses y tienen su fiscalidad. Como los intereses se reciben a vencimiento solo se paga en el IRPF del año del vencimiento de la Letra. Los intereses no tienen retención y se comunican en la Base del ahorro del IRPF con un tipo impositivo entre el 19% y el 23%. Aquí un tema importante con respecto a la emisión de una L9 y L12 antes de fin de marzo de un año específico. La L9 tendría vencimiento 2023 y por tanto los intereses pagarán impuestos en Junio 2024 mientras que la L12 tendría vencimiento 2024 y los impuestos se pagarán en Junio 2025. ¿Qué quiere decir esto? Que hay 365 días de más dónde yo puedo invertir los impuestos de la L12 y generar nuevos rendimientos. Habría que hacer los cálculos para ver qué representaría esto pero se nos haría un artículo más largo de lo deseado, pero lo menciono para tenerlo en cuenta.

 

La paradoja de las letras a 9 y 12 meses

Recapitulando las Letras deberían tener un interés implícito alrededor del tipo de depósito del BCE teniendo en cuenta cómo está éste y cómo se espera que varíe durante el plazo hasta el vencimiento de la Letra.

Pongámonos ahora en Feb 2023 y veamos a qué tipos deberían haber salido las Letras a 3,6,9,12 meses emitidas realmente por el Tesoro teniendo en cuenta las expectativas de tipos de la BCE. Las expectativas consideremos son de subida de 50 bps el 16 de Marzo (esta subida es casi del 100% de probabilidad) y luego dos de 25 bps el 4 de mayo y el 15 de Junio respectivamente y dejemos sin cambios los tipos el resto de meses hasta finalizar en Febrero 2024.

Abajo muestro las rentabilidades a las que se emitieron las Letras la semana pasada y la anterior:

 

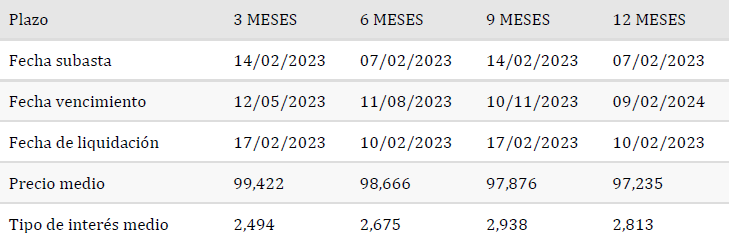
Y con las expectativas arriba señaladas y teniendo en cuenta los días exactas a las fechas del BCE y los cambios de tipos esperados deberían haber salido a los siguientes tipos:

L3: P= 100/ (1+(0,025*27/360+0,03*49/360+0,0325 *8/360)) = 99,336% y salió a 99,422% Tipo Interés medio: 2,863% y salió a 2,494%. (Salió MUY CARA para el inversor)

L6: P= 100/ (1+(0,025*34/360+0,03*49/360+0,0325*42/360+0,035*57/360)) = 98,447% y salió a 98,666%. Tipo Interés medio: 3,121% y salió a 2,675%. (MUY CARA).

L9: P= 100/ (1+(0,025*27/360+0,03*49/360+0,0325*42/360+0,035*148/360)) = 97,643% y salió a 97,876% . Tipo Interés medio: 3,267% y salió a 2,938%. (MUY CARA).

L12: P= 100/ (1+(0,025*34/360+0,03*49/360+0,0325*42/360+0,035*239/360)) = 96,761% y salió a 97,235%. Tipo Interés medio: 3,31% y salió a 2,938% .(MUY CARA).

Como vemos todas las Letras salieron muy caras con esas expectativas de tipos, que igual eran muy optimistas en cuanto a las subidas de tipos . ¿Qué pasaría si quitásemos la última subida de 25 bps? (os dejo los cálculos a vosotros) y os doy el resultado solamente del tipo de interés medio:

L3: 2,863% (sin cambios porque vence antes de la última subida de Junio 2023). MUY CARA.

L6: 3,043% (salió MUY CARA también).

L9: 3,128% (salió algo CARA).

L12: 3,146% (salió MUY CARA).

Con estos datos es normal que el Tesoro Español adjudicara 275% más de nominal en la L12 que en la L9.

Ahora vamos a considerar las expectativas de tipos que tenía el mercado cuando se hicieron las emisiones de estas 4 Letras y con esto se dará la verdadera respuesta a la pregunta inicial, ¿por qué se pagó más rentabilidad en la L9 que en la L12?

Las expectativas de mercado las voy a tomar de la cotización de los futuros del Euribor a la fecha de la emisión y considerando un spread medio de 0,20% entre el tipo que ofrecen las letras y el tipo implícito del Euribor; a este spread se le denomina TED spread (Treasury Bills over Euro libor spread), este spread baja hasta niveles de 0,10% en momentos de tranquilidad en los mercados y sin incertidumbres visibles en el horizonte y puede llegar a 100 bps (o donde le dé la gana al mercado) en épocas muy turbulentas.

No voy a mostrar los cálculos de estas expectativas porque excedería del objetivo de este artículo, pero con esas expectativas del mercado obtendríamos:

L3: 2,683% (salió CARA pero no tanto).

L6: 2,868% (salió MUY CARA también).

L9: 3,102% (salió CARA pero no tanto).

L12: 3,073% (salió MUY CARA también).

Con el cálculo de expectativas de mercado en la fecha de emisión de las Letras vemos que la L9 salió 16,4 bps por debajo de lo teórico (con mi TED spread) mientras que la L12 se emitió 26bps más cara, es decir, se repite que la emisión de la L12 tenía mucho más sentido para el Tesoro y por eso emitió mucho más que la L9 (mi experiencia de años de negociar con el Tesoro Español es que esta “gente” sabe perfectamente lo que hace y no da puntada sin hilo y lo que hicieron fue ahorrar mucho dinero al Estado emitiendo mucho más de la L12 que la L9).

Hay otra característica que es la explicación de la pregunta, vemos que la L12, con las expectativas de mercado, salía teóricamente por debajo de la L9 (3,073% la L12 vs 3,102% la L9) pero NO porque había expectativas de que bajaran los tipos sino porque la L9 se emitió 7 días más tarde que la L12 ( 7 Feb la L12 y 14 Feb la L9) y en esos 7 días las expectativas de tipos subieron unos 15bps debido a que los datos de inflación no fueron buenos y algunos discursos de miembros de los Bancos Centrales de EEUU y EU. Esto es, la L12 se emitió con unas expectativas de tipos más bajas que la L9 y por eso salió a un tipo inferior.

De hecho, si vemos como cotizan en secundario estas Letras en ningún momento la L12 cotiza por debajo de la L9, el 16 de Febrero en el mercado BME SEND cotizaban las letras a los siguientes tipos:

L3: 2,53%

L6: 2,81%

L9: 3,01%

L12: 3,03%

Como vemos en secundario las Letras cotizan muy cerca del valor que he calculado a esas mismas fechas según las expectativas de tipos que tenía el mercado, solamente 0,05% más bajo para la L6 y L12 , 0,09% para la L9 y algo más 0,15% para la L3.

 

CONCLUSIONES

1.- Las letras cotizan según las expectativas de tipos de depósito de la BCE. Estas expectativas se pueden obtener del mercado o tenerlas uno mismo, normalmente el mercado no hace expectativas binomiales, es decir, o 100% ó 0% de probabilidad a una determinada subida sino que otorga probabilidades a las subidas; por ejemplo el mercado no está dando una probabilidad del 100% a que el BCE suba tipos 50 bps en Marzo a pesar de que el BCE lo da por hecho, el mercado está valorándolo con una probabilidad del 70% más o menos (lo cual me parece poco). Posteriormente, el mercado está descontando que el máximo de tipos que llegará el BCE es 3,50% (aunque no lo está descontando al 100%) en el último trimestre de 2023 y luego irá bajando poco a poco hasta estabilizar el tipo BCE en el 2,50%.

Pregunta: ¿Dónde está la Rentabilidad actual del Bono Alemán a 10 años o incluso a 30 años? Exactamente en el 2.50% que es el valor medio de la cadena (Strips) del Euribor a 3 meses reduciendo un valor medio del TED spread de unos 0.20%, o lo que es lo mismo el Bono alemán a 10 años está valorado a lo que el mercado espera que se podría obtener invirtiendo y reinvirtiendo en Letras alemanas a 3 meses durante los siguientes 10 años (lo mismo diría del Bono Español y las Letras a 3 meses españolas). A estos cálculos intermedios de tipos conociendo los tipos Spot a diferentes plazos del mismo activo financiero se le conoce como Bootstrapping. Si, a una misma fecha, sé el valor de la Letra a 3 meses y a 6 meses puedo calcular como debería estar la letra 3 meses dentro de 3 meses para que me diera igual invertir a 3 meses y reinvertirlo todo otra vez a 3 meses dentro de 3 meses o invertir directamente a 6 meses. Si el valor de 3 meses en 3 meses lo considero alto (e irrealizable) entonces invertiré en la Letra a 6 meses y si lo considero bajo (por tanto, espero un tipo superior) invertiré en la Letra a 3 meses y luego lo reinvertiré a ese tipo (espero) más alto de lo que el mercado descontaba y ganaré más rentabilidad que si hubiera invertido en la letra a 6 meses.

Ejemplo simple: tengo 1000 eur para invertir y la L3 y L6 cotizan ambas al mismo tipo del 3%, es decir el mercado descuenta que el tipo a 3 meses dentro de 3 meses esté al 3% también (en realidad algo más bajo por la capitalización pero hagámoslo simple). Si yo espero que en 3 meses el BCE suba tipos al 3.25% es mejor invertir 3 meses al 3% y luego (si tengo razón y los tipos suben) invertir otros 3 meses al 3.25%. Está claro que esta inversión es mejor que haber invertido el dinero a 6 meses al 3% durante todo el plazo. Y esto es la base del mercado, de TODOS los mercados y de (casi) todos los activos, por ejemplo, saber qué descuenta el mercado para dar un valor a un activo y si considero que descuenta algo irrealizable (por ejemplo Dividendos muy altos en el futuro, o Ebitdas muy altos) vender el activo, y si descuenta algo que considero que realmente va a ser mejor, comprar el activo.

2.- Si se va a invertir en el mercado primario (vía el Banco de España o con su propio banco) es mejor antes ver cómo cotiza en el mercado secundario (BME SEND) porque igual es mejor comprar en secundario (si es posible y analizando comisiones etc). Muchas veces el mercado primario está caro porque los bancos están obligados a comprar (son creadores de mercado), quieren quedar bien con el Tesoro , tienen volúmenes que no se consiguen en secundario y tienen órdenes de sus clientes (no competitivas) y quieren comprar a tipo competitivo (más alto) y venderlo a tipo no competitivo (más bajo) y ganar más dinero (además de las comisiones).

Por tanto, quieren asegurarse de comprar por encima del tipo no competitivo (su ideal es obtener el tipo marginal).

3.- En el caso de la última subasta de L9 y L12 la demanda en la L12 fue muy fuerte por parte de inversores minoristas y eso probablemente tiró (incluso más a la baja) la rentabilidad del L12. En definitiva, el tipo medio de la L12 salió por debajo del L9 en 0,125% (12.5 bps de tipo medio) porque, como he dicho, las expectativas de tipos subieron cuando se emitió la L9 una semana más tarde que la L12 pero también una parte fue la fuerte demanda de la L12 que se ve en la diferencia entre tipo medio y marginal de 2,6bps en la L12 y de 3,5bps en la L9. La fiscalidad, como he comentado, también juega aquí porque la L9 se emitió antes de fin de marzo y por tanto paga impuestos en IRPF 2024 (contra IRPF2025 la L12) pero no sabría decir en cuánto pesa este factor. El 85% de la explicación viene por el cambio de expectativas entre la emisión de la L12 y la L9 y el restante es la fuerte demanda de la L12.

4.- El problema del minorista es que tener dinero en la cuenta corriente al 0% es peor que invertir en una Letra aunque ésta sea cara pero aún así, siendo esto cierto, la estrategia es clara, i.e, invertir en la letra de más corto plazo, L3, hasta que se vea que el mercado ya empieza a descontar que los tipos no van a subir más y en ese momento reinvertir el dinero en una L12. Por ejemplo, en Febrero creo que la estrategia correcta hubiese sido invertir todo en la L3 (aun siendo cara al 2,494%) porque espero que el BCE suba tipos 50bps en marzo y por tanto la L3 se podrá reinvertir cerca del 3% en mayo y a partir de ahí reinvertir de nuevo en una L3 en Agosto y finalmente reinvertir todo en L12 en Noviembre 2023 hasta Noviembre 2024. En un movimiento alcista de tipos hay que reinvertir en vencimientos cortos para reinvertir en tipos más altos e, inversamente, invertir en vencimientos largos cuando los tipos estén cerca de, o, en sus máximos.

Bueno espero haber clarificado un poco el funcionamiento de este mercado olvidado durante años con los tipos al 0% o negativos pero que ahora está tan de moda, con razón, con los tipos cercanos al 3%. Si hay algo que nunca hay que olvidar es que cuando alguien ofrece rentabilidades muy buenas y parece que sin riesgo, eso no existe (sellos, bosques, vinos etc etc) y por último que los depósitos hasta 100.000€ en los bancos de la Eurozona están garantizados por el Fondo de Garantía de Depósitos y que son una alternativa a las Letras siempre que sea un banco regulado por el Banco Central del país de la eurozona.