Por Óscar Gil Flores, profesor del IEB.
Para la medición del riesgo de un producto financiero, un fondo o una acción, utilizamos la métrica de la volatilidad. La volatilidad cuantifica el riesgo, tal que a mayor volatilidad, mayor es el riesgo asumido con la inversión y mayor su capacidad de pérdida. Pero para analizar el riesgo, tenemos que ir un poco más allá.
Si uno toma las rentabilidades históricas diarias de un activo o fondo de inversión, y gráfica un histograma, verá una forma acampanada que se parece, aparentemente, a una distribución normal.
Pero casualmente, si pintamos encima de los datos históricos una distribución normal, con igual media y desviación típica que las rentabilidades, veremos importantes diferencias. Los datos observados exceden a la curva normal en la zona central y en los extremos, y es en la zona intermedia donde la curva normal acumula mayor probabilidad que los datos.
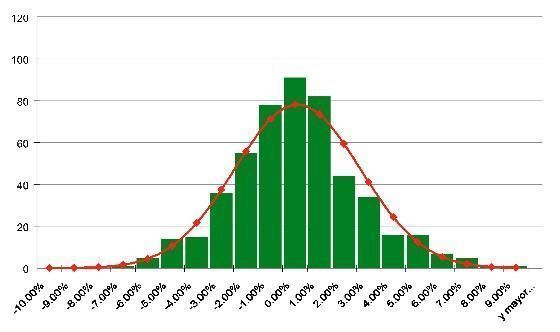
Este efecto se recoge en la curtosis (o momento centrado de orden 4 para los estadísticos). Si el exceso de curtosis es positivo, como es el caso de los datos del mercado, esto implica que los eventos extremos, en realidad, son más probables de lo que predice una distribución normal. Estos extremos, especialmente los vinculados con pérdidas, que aparecen con mayor frecuencia de lo esperado, supone un riesgo adicional, que no se contempla en la métrica de la volatilidad o desviación estándar.
Es decir, no es suficiente con analizar la volatilidad de un producto, si no que adicionalmente, hay que ver si tiene curtosis, es decir, este efecto por el cual, los eventos extremos son incluso más probables de lo que podríamos establecer con la distribución normal.
Seguro que muchos recuerdan que entre la media más menos una desviación estándar para la distribución normal hay un 68% de probabilidad. Entre la media más menos dos desviaciones estándar un 95,5% y entre la media más menos 3 desviaciones estándar el 99,7%.
Así, más allá de 3 veces la desviación estándar, sólo debería haber un 0,3% de los datos, es decir, 3 de cada 1000. Pues la curtosis lo que indica es que esta estimación se queda corta, y que el número de observaciones puede llegar a ser bastante superior. Un dato, por tanto, a tener en cuenta.
Esto es tal y como se indica, para la mayoría de acciones y bonos… y, por tanto, los fondos y ETF que invierten en estos subyacentes.
El mercado históricamente había aplicado la distribución normal para el análisis del riesgo y la posibilidad de pérdidas en los activos financieros. Bajo este modelo, las pérdidas se limitaban poco más allá de 3 veces la volatilidad.
Esto fue así hasta un lunes (¡como no!), el 19 de octubre de 1987, ahora hace 30 años. Ese día, el Dow Jones cayó un 22,6%, fuera del rango que podía contemplar la distribución normal. Ese mismo día Hong Kong había caído un 45,8% y España un 31%. Esas importantes caídas no sólo impactaron en los ahorros de multitud de inversores, sino que sacudieron a la normal del centro de la modelización probabilística para las rentabilidades.
A partir de esa misma semana es posible observar uno de los efectos que tiene la curtosis en el mercado: el smile (o skew) de volatilidades. Con el smile de volatilidad, el mercado sigue utilizando la distribución normal, pero con distintos niveles de volatilidad para cada strike, adaptándose así la distribución real de las rentabilidades del mercado.
Con toda probabilidad, la curtosis es consecuencia del comportamiento humano, que genera los impulsos de venta o compra masiva y, por tanto, estuvo en el mercado desde siempre. Sólo que la curtosis hizo acto de presencia en el mercado, con una puesta de escena impactante, ahora hace poco más de 30 años.

Estás en Inicio » Actualidad » Blog » Treinta años de la curtosis en el mercado